FISIDABO

Comparteix:

Mesura de distàncies

 

 

 

Mesurar la grandària d'un objecte petit és fàcil: podem utilitzar una cinta mètrica. La cosa es complica quan les distàncies que volem mesurar són més grans. Com podem mesurar l'alçària del nostre col·legi? Amb una cinta mètrica és bastant difícil. Us explicarem com mesurar distàncies grans de dues formes:

Cal dominar les dues tècniques abans de pujar al parc d'atraccions, ja que són complementàries: en alguns experiments utilitzarem la primera, en d'altres la segona. Evidentment, si coneixeu qualsevol altra aplicació també la podeu utilitzar.

Inclinòmetre i trigonometria

Els mètodes que us proposem en aquest apartat són els que s'utilitzen des de fa més de dos mil anys. Més o menys modificats, amb més o menys matemàtiques. Podríeu pensar que avui en dia amb el GPS aquests mètodes ja no s'utilitzen... doncs aneu ben equivocats/des: són molt més precisos que el GPS. A més... com creieu que es construeixen els túnels on no arriba el senyal dels satèl·lits?

Suposem que volem mesurar l'alçària h de l'edifici del nostre col·legi... sense utilitzar una cinta mètrica gegantina. El que podem fer és demanar ajuda a la trigonometria. Imaginem que ens separem una distància d de la paret de l'edifici. Ara mesurem l'angle β que forma la horitzontal amb el punt més alt de l'edifici. El que tenim, d'una forma esquemàtica és el següent:

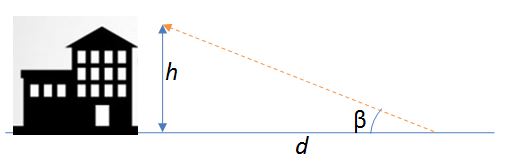
La distància d és molt fàcil i còmoda de mesurar. Per mesurar l'angle β farem servir un inclinòmetre. Tranquils, que us expliquem què és! Agafarem un semicercle graduat, o utilitzarem la plantilla que podeu descarregar aquí. Del centre del semicercle penjarem un pes amb un fil,  de forma que en inclinar el nostre inclinòmetre el pes quedi vertical i ens marqui l'angle així:

 

(Font de la imatge: WikiHow)

Ara només cal fer una mica de trigonometria per tal de calcular l'alçària h. Si la tangent de l'angle β en aquest cas és tanβ=h/d, aïllant l'alçària, que és la longitud que volem mesurar, obtenim:

h = d tanβ


Tingueu en compte, però, que aquesta mesura seria certa si esteu mesurant amb el cap tocant el terra. Postura força incòmoda. Normalment, però, estareu drets fent la mesura. Per tant a l'alçària h que mesureu caldrà afegir l'alçada fins als vostre ulls. Podeu agafar aquesta alçada com a metre i mig si no n'esteu segurs. No us preocupeu, l'error en l'angle serà més gran!

Experiments proposats:

L'alçària de la teva escola.

El primer experiment que us proposem no podia ser altre que mesurar l'alçària de la vostra escola. Per fer això només cal construir l'inclinòmetre, separar-se de l'edifici una distància d i mesurar l'angle.

... i l'alçària d'una muntanya?

No necessitareu mesurar coses tan complicades al FISIDABO, però... com mesurar l'alçària d'una muntanya si no tenim accés a la seva base? Us donem una pista: cal mesurar dos angles en comptes d'un! (podeu mirar una proposta de solució aquí!)

L'aplicació ImageMeter

Una altra forma de mesurar distàncies molt senzilla és a partir d'una fotografia. El principal problema d'aquest mètode té un nom: perspectiva. Això fa que els objectes llunyans semblin més petits, i els propers més grans. La forma més senzilla per tenir aquest efecte en compte és que a la fotografia aparegui alguna referència el més propera possible a l'objecte del que volem mesurar la grandària. Siguem pràctics, podem un exemple. Suposem que volem mesurar el radi d'una roda de fira com aquesta:

 

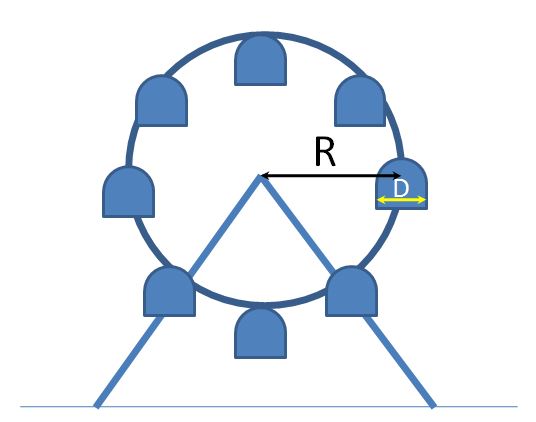
Per fer-ho podem utilitzar una cinta mètrica molt llarga i algunes habilitats d'escalada... o més fàcil. Mesurem còmodament el diàmetre d'una de les cistelles. Fem una foto en la que es vegi tota l'atracció, i utilitzant una senzilla regla de tres podem saber la mesura del radi. La bona notícia és que hi ha moltes aplicacions de mòbil que fan aquesta regla de tres per nosaltres, directament a partir de la fotografia. La que utilitzarem nosaltres és ImageMeter, però podeu utilitzar-ne qualsevol altra. Trobareu un vídeo (en anglès) que explica com funciona aquesta aplicació aquí. Aquí us expliquem el bàsic que cal saber per utilitzar-la al Fisidabo:

    • En primer lloc cal que obrim la foto amb la icona de la fotografia. Un cop fet podeu clicar a la icona ✓.
    • Ara ja la teniu al menú principal de l'aplicació. Si feu clic a sobre l'obrireu.
    • Ara necessitem donar a l'aplicació la mesura d'algun objecte, com podria ser el diàmetre de la cistella de la roda de fira. Per fer això feu clic sobre la icona + per afegir una referència. S'obrirà un menú:
    • Seleccioneu "reference scale", poseu el dit sobre un dels extrems del vostre objecte de referència i desplaceu-lo fins a l'altre costat. En el nostre cas ho hauríem de fer de banda a banda de la cistella. No us preocupeu si no heu tingut punteria... després l'aplicació us deixarà canviar els punts i fer un zoom de la fotografia!
    • L'aplicació ens preguntarà llavors quina és la distància de l'objecte de referència. Afegiu-la.
    • Ara amb la icona ↔ podeu clicar i arrossegar el dit entre qualsevol parell de punts de la foto que vulgueu mesurar. En el nostre cas el radi de la fira de roda.

I ja teniu la distància que volíeu! Si us atreviu, també podem tenir en compte la perspectiva si l'objecte no està just davant de nosaltres. Per fer això només cal afegir una "perspective reference"...

Experiments proposats:

L'alçada de la teva escola. Un altre cop.

Torna a mesurar un altre cop l'alçària de la teva escola, aquest cop amb l'aplicació ImageMeter. Poc més cal afegir.

Mesura les dimensions d'un quadre.

Si voleu utilitzeu l'opció per mesurar en perspectiva, podeu fer la fotografia d'un quadre que tingueu a casa. Ara intenteu amb l'app determinar les seves dimensions.